Materials for future nuclear applications all share one important property: the ability to maintain functionality during exposure to extreme levels of irradiation. Developing such materials requires an in-depth understanding of the atomic processes that attribute to the build-up of radiation damage.
 |
| Materials for future nuclear applications all share one important property, the ability to maintain functionality during exposure to extreme levels of irradiation. |
ANSTO’s study used atomistic scale simulations to discover the mechanisms of initial defect formation. Allowing a first-hand look at which factors contribute to a material’s radiation tolerance or susceptibility will help us understand and design prospective nuclear materials.
The virtual microscope
To aid the understanding of a macroscopic process, it is important to isolate and study the contributing microscopic factors. Applying this philosophy to understanding how a material responds to radiation, inevitably leads us to the investigation of the fundamental atomic-level phenomena. However, the dynamics of radiation damage cannot be observed directly even using the best experimental techniques: the processes are simply too small and too fast.
This is where ‘virtual’ experiments can take over. Atomistic computer simulations are becoming increasingly popular, aided by advances in High Performance Computing (HPC). The ability to model the motions of millions of atoms over the nanosecond timescale has resulted in simulation becoming a powerful tool to complement experiment.
The investigation of radiation damage is well suited to computer simulation, in particular molecular dynamics (MD). In MD, each atom in the system is treated individually, allowing us to follow the trajectories of energetic atoms and reveal the mechanisms of damage accumulation (see Fig. 1). In our research, we develop new techniques based on MD computer simulation.
We study low-energy radiation events with the goal to understand which factors contribute to changes in initial defect formation. Combining this methodology with thousands of processors from HPC facilities has allowed us to gain a very high level of statistics enabling precise calculation of important quantities such as the threshold displacement energy.
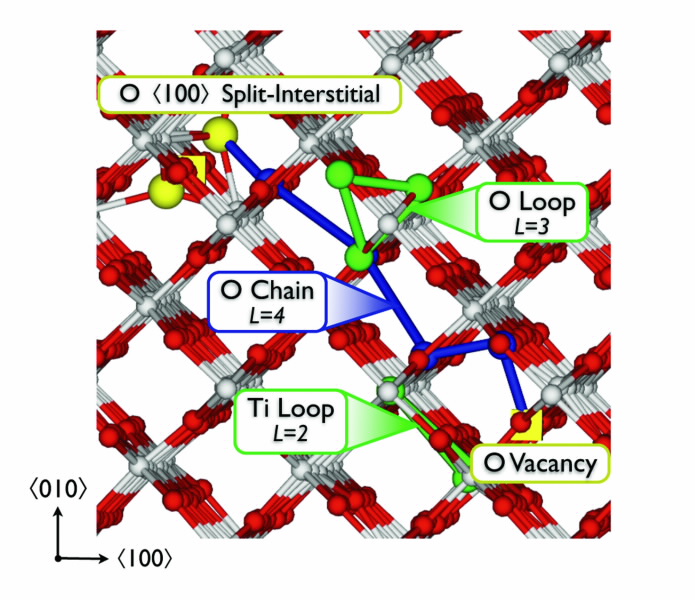 |
Fig 1. A snapshot of an MD simulation inrutile. By tracking the tracjectories of the atmos, the mechanisms of defectroduction and recombination are revealed. In this simulation, an oxygen split- interstitial is formed (yellow) by a succession of knock-on events referred to as a replacement chain (blue). When these chain form loops (green), no defects are produced. |
The threshold displacement energy
What is the kinetic energy required to permanently displace an atom in a particular system? This question forms the basis for numerous models of radiation damage and the answer is known as the threshold displacement energy or Ed. A common use of Ed is in SRIM (The Stopping and Range of Ions in Matter)[1] a popular computer simulation program. SRIM is used extensively by the semiconductor industry and ion-implantation community to calculate ion-implantation depths, defect production and sputtering yield.
However, the accuracy of models such as SRIM hinge on ascertaining an accurate value of Ed. To precisely determine Ed requires a methodology that can capture the onset of defect creation. This methodology would be required to sample numerous variables such as impact energy and direction. Due to the probabilistic nature of defect production at low energies, a very high level of statistics is required to enable an accurate extrapolation of Ed [2,3]. The methodology we have developed not only meets the above criterion but does so in a generalised and transferable manner. This allows us to seamlessly change the material under investigation and generate readily comparable results.
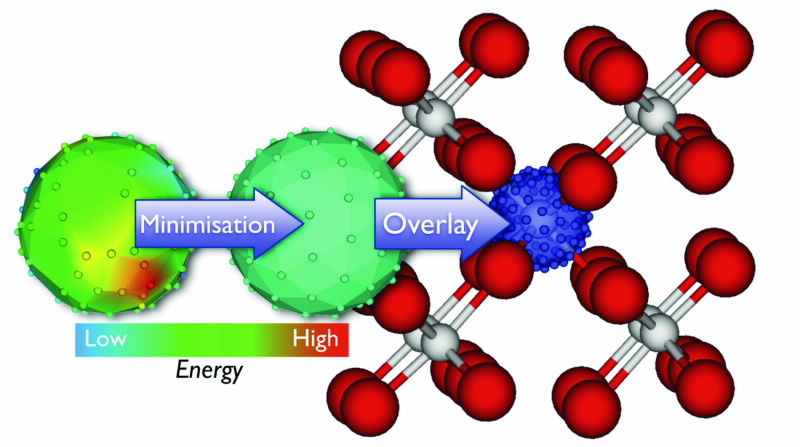 |
| Fig 2. The generation of directions of initil impact from soluions to 'The Thomson Problem'. Firstly the points are randomly distributed on the surfce of the sphere. After assigning a repulsive potential to each point, the configuratin is minimized to produce a uniform distribution. The sphere is then centred on an atom (as shown fo a Ti atom in the rutile lattice) so that each point creates a vector of initial impact. |
New solutions to an old problem
The main feature of our methodology that enables transferability is the automated generation of directions of initial impact. This allows any crystal type to be the subject of investigation, regardless of the complexity of the structure. To achieve this, inspiration was drawn from a problem of historical significance, namely “The Thomson Problem”.
In 1904, J.J. Thomson outlined the problem of uniformly distributing points on the surface of a sphere whilst attempting to determine the arrangement of point charges in the atom [4]. Since then the problem has become a significant area of research, applicable to a multitude of real-world problems from the structure of fullerenes to the morphology of viruses.
Importantly, solutions to the Thomson Problem can be employed as a method of sampling directions of initial impact. This is shown in Fig. 2, where 100 points are uniformly distributed on the surface of a sphere and then superimposed on top of an atom providing vectors of initial velocity.
Taking a look at TiO2
The three common polymorphs of TiO2: rutile, brookite and anatase, provide ideal candidates to test our newmethodology, allowing us to study the effect of crystal structure on initial defect formation. Furthermore, rutile TiO2 is a constituent phase in Synroc, the wasteform developed by ANSTO for the immobilisation of radioactive waste.
Experiments by ANSTO researchers have shown surprising differences between the polymorphs, with rutile being highly radiation tolerant, while anatase was easily amorphised [5]. This important result provides a solid foundation for comparison to our simulations.
Our study into the TiO2 polymorphs involved over a quarter of a million MD simulations, with Fig. 3 demonstrating the importance of good statistical sampling. Displacement events along a single direction (Fig. 3a) suffer large uncertainties due to the chaotic nature of the collision process. However, the problem is eliminated (see Fig. 3b) when the directions are sampled using solutions to the Thomson Problem.
Another benefit from achieving a high level of statistics is the capability to carry out detailed analysis. A prime example of this is shown in Fig. 4, which shows a comprehensive categorisation of the residual defect clusters created from simulations in rutile.
The calculated defect proportions give quantitative support to an observation common to all polymorphs, that significantly more isolated oxygen point defects are created than titanium point defects. This relates to the ease at which displacements occur on the oxygen sublattice resulting in long-range replacement chains.
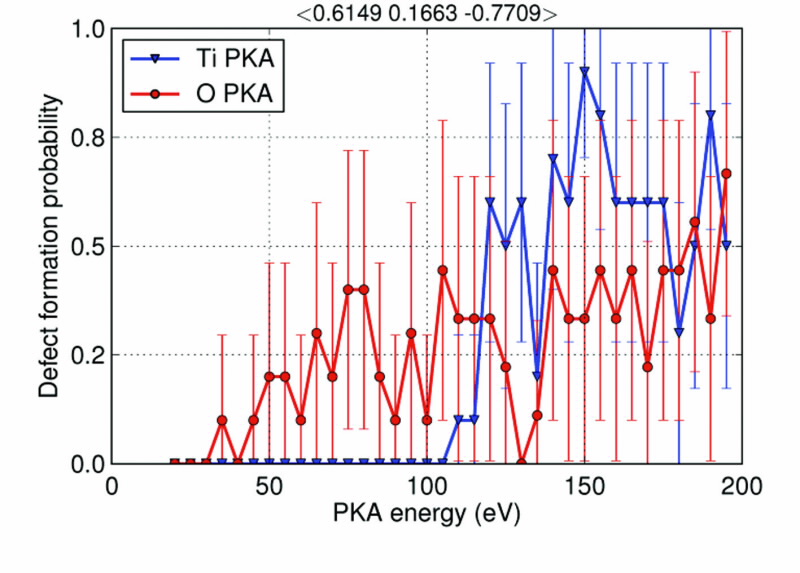 | 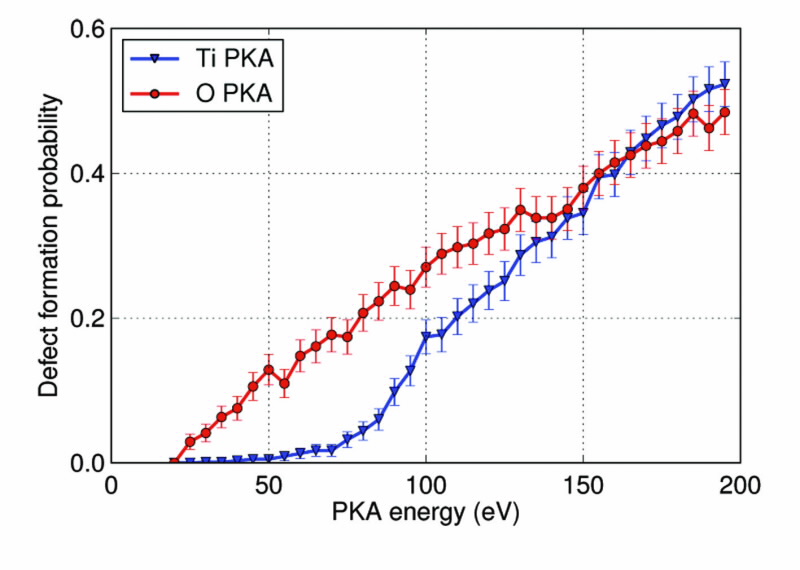 |
| Fig 3. Defect formation probability as a function of energy of the impacted atom her referred to as the PKA (primary knock-on atom). (a) Sampling a single impact direction. (b) Sampling 100 directions uniformly distributed othe surface of a sphere. |
Future directions
The methodology we have developed is applicable to any crystal structure, enabling a quantitative approach to investigating radiation damage. In future studies, we will employ this approach to study complex materials such as pyrochlores to aid the understanding and design of prospective nuclear materials.
The present work also forms the foundation for further studies into the dynamics of defect recombination over longer time scales. Working in conjunction with Los Alamos National Laboratory, we aim to build the complete picture of the atomic-level response to
radiation damage.
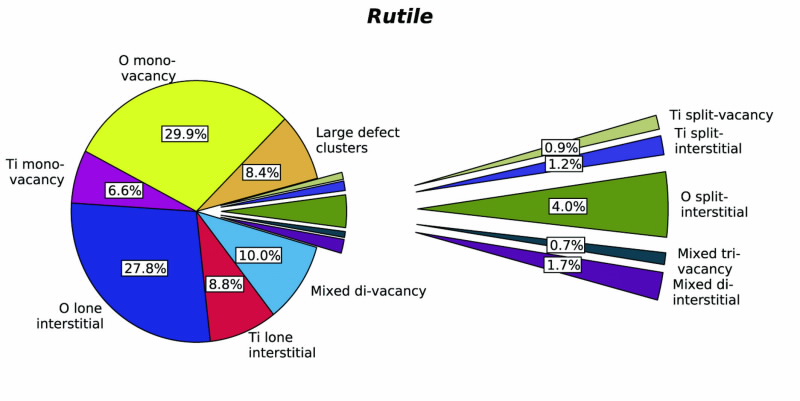 |
| Fig 4. Residual defect clusters in rutile. Note the larger proportion of isolated oxygen vacancies and interstitials, a result of long chains of atmoic replacements on the oxygen sublattice. |
References
- J. F. Ziegler, M. D. Ziegler, and J. P. Biersack, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 268, 1818-1823 (2010).
- K. Nordlund, J. Wallenius, and L. Malerba, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 246, 322-332 (2006).
- L Malerba, JM Perlado, A. Sánchez-Rubio, I. Pastor, L. Colombo, and T. Diaz de la Rubia, Journal of Nuclear Materials 283, 794–798 (2000).
- J. J. Thomson, Philosophical Magazine Series 6 7, 237-265 (1904).
- G. R. Lumpkin, K. L. Smith, M. G. Blackford, B. S. Thomas, K. R. Whittle, N. A. Marks, and J. Z. Zaluzec, Physical Review B 77, 1-9 (2008).


