Researchers from ANSTO's energy project team at the Bragg Institute have been modelling ice cages to determine their potential for safely storing hydrogen.
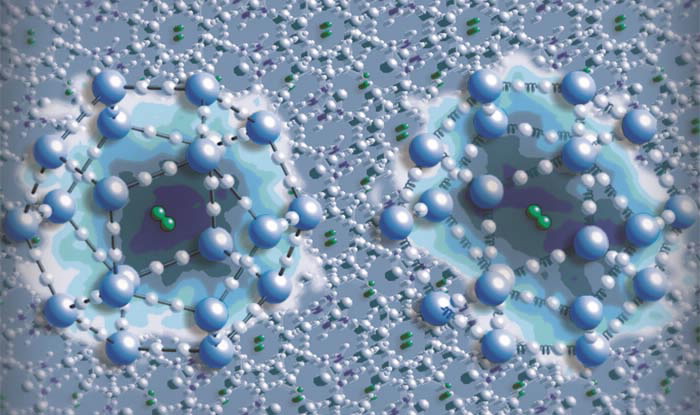 |
| Hydrogen gas molecules (pairs of green balls) trapped inside a clathrate hydrate. Inserts (left to right): potential energy surfaces (dark blue background) around a hydrogen molecule in the “rigid” and “flexible” clathrate hydrates respectively. There is dynamic coupling between the hydrogen molecule and a flexible clathrate hydrate encapsulating it which may play an important role in the hydrogen storage capacity of the hydrate. |
Introduction
Environmental sustainability is driving energy production and use towards cleaner and greener technologies such as using hydrogen as a fuel. However, this raises the problem of how best to safely store hydrogen.
This study investigated trapping hydrogen molecules (H2) in ice. This forms a clathrate hydrogen hydrate, which is essentially an ice cage which can hold hydrogen.
Although this research focuses on ice, there are other options for cage materials and we need to understand how the hydrogen interacts with the container carrying it. This is best done by analysing how the hydrogen molecules move around in the cage. The research also tackled the question of whether the cage’s own thermal motion is also important.
Although complex, these questions must be understood because they relate directly to the performance and safety of the hydrogen storage material. This research used a more rigorous approach than has been commonly used previously, taking into account the cage’s flexibility rather than assuming that the cage is rigid. This has highlighted the shortcomings of previous experiments.
It is crucial to correctly calculate the interaction between the hydrogen and the cage so that we can work towards ice composite materials that can safely store more hydrogen.
Hydrogen in a clathrate hydrate cage: A hydrogen-storage system
Environmental sustainability is driving energy production and use towards cleaner and greener technologies. This has brought to the forefront of research the prospect of a hydrogen economy, in which the hydrogen molecule is the primary energy carrier with its conversion to power through fuel-cell technologies.
An important challenge in moving to a hydrogen economy for the automotive industry is the onboard storage of hydrogen through a technology which meets both power (as capacity) and delivery time (fuelling) requirements of the vehicle.
The small hydrogenmolecule is energy-intensive to compress, and the limitations of high pressure storage tanks have been circumvented by storage of hydrogen within another material.
Candidate materials include metal hydrides, chemical hydrides, and porous materials such as coordination frameworks and hydrogen clathrates [2], but to be of practical use, these should meet the US Department of Energy (DOE) targets [3] for both storage capacity and delivery of the hydrogen, and should be be cheap, non-toxic, compact, and light, for viable commercialisation.
The structure of type II pure hydrogen clathrates, (Fig. 1), form and remain stable only at 200 MPa and 273 K [4].
This pressure is high, but can be reduced by incorporating other molecules in the nanocages, e.g. tetrahydrofuran [4].
However, adding other molecules into the clathrate means that there is less room for the hydrogen and the conflicting requirements of structural stability and storage capacity are difficult to reconcile.
For a pure hydrogen hydrate, the theoretical maximum storage capacity is close to the 5.5 w/w% DOE storage requirement for 2015 [3], assuming 2 and 4 hydrogen molecules in the small and large cages respectively (see Fig. 1) [5].
The prospect of reaching this maximum relies on an understanding of the nature of the interactions between a guest molecule and the cage containing it.
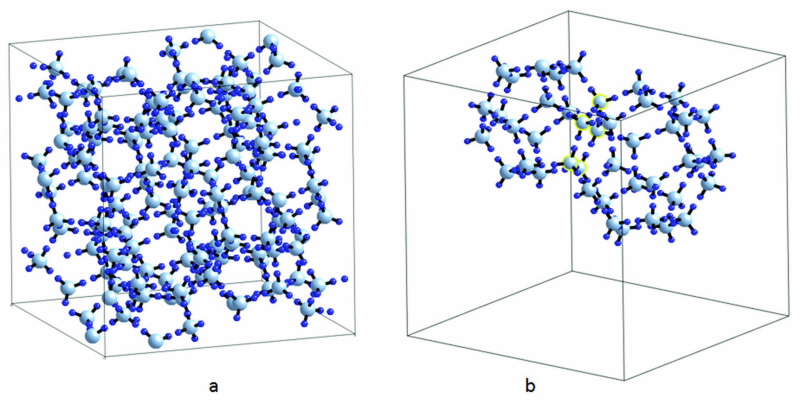 |
| Fig 1. Schematic of structure II hydrogen hydrate cages as (a) the unit cell, and (b) part of the unit cell highlighting small and large cages. There are 16 small and 8 large cages in a unit cell. The small dark blue circles are H atoms and the large light blue are O atoms. The two cage types share a pentagonal face which is highlighted in yellow. Guest hydrogen molecules are not shown for clarity. |
There is a sweet spot in the interaction between the hydrogen guest and the cage that maximises storage capacity and allows the gas to be released for subsequent use.
When the hydrogen molecule is loosely held, it undergoes a fascinating phenomenon known as quantum translation/rotation that has been widely studied theoretically [6]. However, these studies assume that the cage is rigid in order to simplify the problem computationally, since including the movements of the cage complicate these calculations [7].
We resolve these difficulties by taking an axiomatic approach which enables us to model this quantum system classically, at 15 K, using ab initio molecular dynamics (MD) in VASP [8].
Quantum systems are more sensitive to changes in the hydrogen-cage interaction than classical systems.
By treating the system classically (which is easy) and comparing results from a flexible-cage calculation with that for a fixed-cage calculation, we can assess any differences and judge if ignoring cage flexibility in the real quantum system will cause a serious error.
There are four types of motion that are of importance here.
The hydrogen may rotate around its centre (twist) and translate (rattle) in the cage. The cage is more restricted in its motion and we consider libration, which is restricted rotation (or twisting) of the two H-atoms about an axis through the O-atoms.
We also consider a translation (more like shaking) of the water molecule about its average position in the cage.
A useful quantitative measure of the interaction between the hydrogen guest and the cage is the potential of mean force (PMF) which is calculated from the MD atomic trajectories as the negative logarithm of the population density of the hydrogen molecule within the cage.
In the following sections we look in detail at the atomic and molecular motions obtained from the MD simulations to extract what interactions exist and their origins.
Where is the guest?
Fig. 2 shows the first and perhaps most convincing result from the MD simulations for a hydrogen molecule in a fixed and flexible cage. There are clear differences: Firstly, the PMF of the hydrogen in the flexible cage shows that the hydrogen covers a larger spatial range compared to that of the hydrogen in the fixed cage.
Secondly, whereas the fixed cage PMF is approximately isotropic, the flexible cage PMF has a more complex structure, which shows that there are important interactions in the guest-host dynamics.
This result demonstrates that the fixed cage computational approach fails to capture some essential physics of the guest-host interactions and is a poor starting point for understanding the technologically important storage-capacity issues.
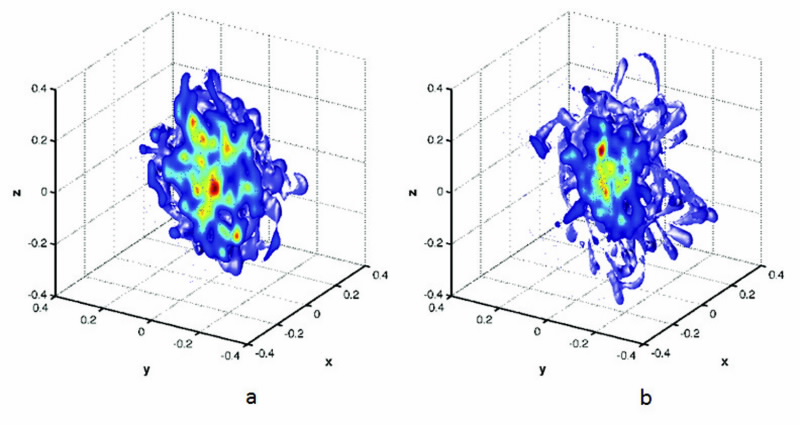 |
| Fig 2. Cross-sections through the 3D potential of mean force (PMF) for the H2 guest in the (a) fixed cage and (b) the flexible cage, where the contours show greater depth in energy from red to blue. This result demonstrates that the fixed cage computational approach fails to capture some essential physics of the guest-host interactions and is a poor starting point for understanding the technologically important storage-capacity issues. |
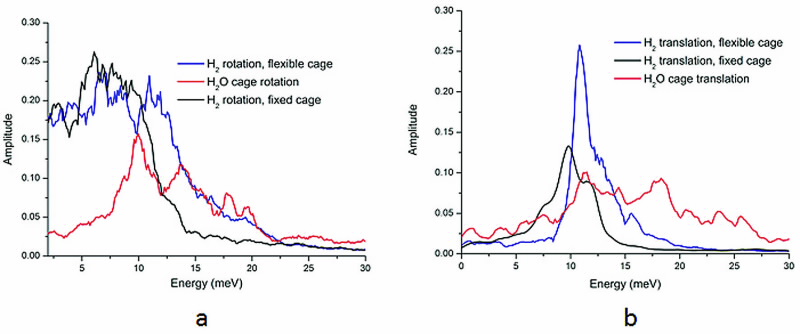 |
| Fig 3. Frequency spectra of the (a) rotational/librational and (b) translational motions of the H2 and the H2O cage molecules. |
It is important to understand the mode coupling because this affects the total energy (stability) of the system via the entropy; a key factor in the storage capacity and temperature range in which the material is useful.
Rotational spectra of H2 in the fixed, flexible deuterated and flexible H2O cages. The fixed and deuterated cages exhibit similar spectral features in the region around 10 meV.
Does the guest rattle the host?
Dynamical coupling between the guest and the cage requires the motions for the two to have similar frequencies and to examine this, we extracted the frequencies of selected dynamical modes of the hydrogen and the flexible cage H2O molecules from the MD trajectories.
The results in Fig. 3 show that both the librational and translational modes of the cage H2O overlap considerably with the rotational and translational modes of the hydrogen, respectively, pointing to significant coupling.
A striking feature of Fig. 3 is the peak at approximately 10 meV which corresponds closely to the well-known peak at 9.86 meV observed experimentally using inelastic neutron scattering.
This peak is normally attributed to the translational motion of the hydrogen (“rattling”) but the current work suggests that this mode contains a rotational contribution, at least from the H2O cage.
How does the guest behave in a heavy host?
Substitution of the hydrogen atoms of the cage with deuterium is routine in inelastic neutron scattering experiments because it effectively removes the signal from the ice.
This makes it easier to study the movements of the hydrogen molecule, but implicitly makes the assumption that movements of the hydrogen guest and the cage are independent.
We investigate the effect of this cage deuteration on the rotational dynamics of the hydrogen (Fig. 4). Compared to the normal H2O cage, the deuterated cage gives rise to a rather different (classical) rotational spectrum for the hydrogen because the coupling to the cage has changed.
It is particularly important to note that the normal H2O and deuterated-cage spectra differ in the region around 10meV.
Our results suggest that deuteration of the cage shifts the cage dynamics to be closer to that observed for the fixed cage system, giving a “false agreement” with a calculated spectrum in which the cage is fixed and that for the experimentally measured deuterated cage.
This is an exciting result that we intend to verify experimentally.
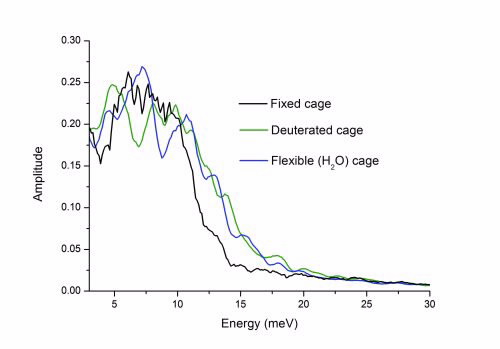 |
Rotational spectra H2 in the fixed, flexible deuterated and flexible H2 O cages. The fixed and deuterated cages exhibit similar spectral features in the region aroudn 10 meV. |
Conclusion
Quantum systems are delicate and it is risky to assume that substituting a normal ice cage by a heavy-water ice cage will not affect the motions of the guest in the cage.
Clearly, it does. This is an important warning because it is common (and convenient) practice to use deuterium substitution to remove the incoherent signal from hydrogen that would otherwise clutter the signal from the H-atoms of interest.
Simulation (as we use) is probably the simplest method of guarding against this mistake.
Previous studies have used analytical expressions for the potential-energy surface for the hydrogen molecule that give very accurate results, but for a fixed-cage model that we have shown to be inadequate.
It would be difficult to use these analytical methods for a model in which the cage is flexible, but we have shown that the more tractable potential of mean force (PMF) for the hydrogen molecule (which is very close to the potentialenergy surface) is very different in the cases of flexible and rigid cages.
This arises because the frequencies of the low-energy motions of the cages almost coincide with the period of the hydrogen motions, which could ultimately be used as a method for tuning hydrogenstorage capacity.
Authors
Elvis Shoko, Vanessa K. Peterson, Gordon J. Kearley
ANSTO
References
- Peterson, V. K., Shoko, E., and Kearley, G. J., The Effect of Host Relaxation and Dynamics on Guest Molecule Dynamics in H2/tetrahydrofuran-hydrate, Faraday Discuss., 151, 37-46 (2011).
- David, W. I. F., Effective Hydrogen Storage: A Strategic Chemistry Challenge, Faraday Discuss., 151, 399-414 (2011).
- DOE. http://www1.eere.energy.gov/hydrogenandfuelcells/storage/pdfs/targets_onboard_hydro_storage_explanation.pdf, the targets for a future hydrogen economy as defined by the Department of Energy.
- Struzhkin, V. V., Militzer, B., Mao, W. L., Mao, H-K., and Hemley, R. J., Hydrogen Storage in Molecular Clathrates, Chem. Rev. 107, 4133-4151 (2007).
- Schuth, F., Hydrogen and Hydrates, Nature, 434, 712-713 (2005).
- Xu, M., and Bacic, Z., Inelastic Neutron Scattering Spectra of a Hydrogen Molecule in a Nanocavity: Methodology for Quantum Calculations Incorporating the Coupled Five-Dimensional Translation-Rotation Eigenstates, Phys. Rev. B, 84, 195445 (2011).
- Patchkovskii, S., and Tse, J. S., Thermodynamic Stability of Hydrogen Clathrates, Proc. Natl. Acad. Sci. USA, 100 (25), 14645-14650 (2003).
- Kresse, G., and Furthmuller, J., Efficient Iterative Schemes for ab initio Totalenergy Calculations Using a Plane-wave Basis Set, Phys. Rev. B54, 11169-11186 (1996); Bloechl, P. E., The Projector Augmented-wave Method, Phys. Rev. B, 50, 17953-17979 (1994); Kresse, G., and Joubert, J., From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method, Phys. Rev. B, 59, 1758-1775 (1999).
Published: 26/11/2012


