Many challenges remain in the development of physical models for gas-liquid flow for different flow regimes, an important aspect in the understanding of the cooling mechanism of a reactor for example.
One approach to unravel such flows is the consideration of a two-fluid model based on the interpenetrating media framework where the inter-phase exchanges of mass, momentum and energy can be modelled as interfacial transfer term acting on each phase.
In this sense, two sets of conservations (one conservation equation for mass, momentum and energy of the gas phase as well as liquid phase) can be written in terms of phase-averaged properties.
The dynamics of the interaction between the two phases are fully described by the constitutive relationships governing the inter-phase mass, momentumand energy exchange.
A standard method is modelling of population balance for the gas-liquid flow. In order to predict the complex hydrodynamics processes of various bubbly turbulent pipe-flow conditions we capture the bubble coalescence and bubble breakage mechanisms, making a complete three-dimensional two-fluid model.
Application of models
Mechanistic modelling of gas-liquid flows allows more realistic predictions of gas-liquid flows, circumventing the need to resort to flow regimes which are empirically determined and do not aptly account for the time and length scale for the flow regime transition between two flow regimes.
Better safety analyses can be performed for gas-liquid flows in existing and advanced nuclear reactors.
Population balance modelling
To overcome the limitations represented by the flow regime approach, the bubble coalescence and break-up phenomena are directly simulated through the consideration of a population-balance equation.
The fundamental development stems from the consideration of the Boltzman equation, which describes the particle-size distribution.
On the basis of this equation, different approaches are derived such as the Average Bubble Number Density (ABND) equation [1], MUSIG model [2] and Direct Quadrature Method of Moment (DQMOM) [3].
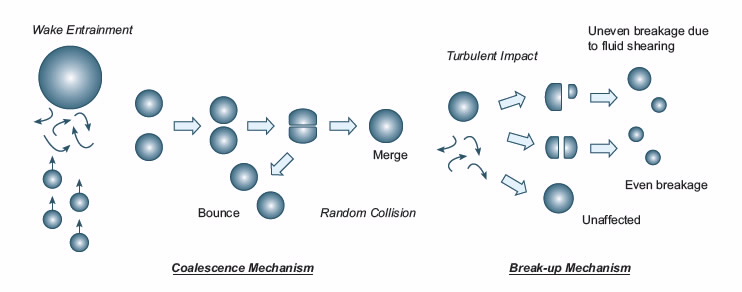 |
| Fig 1. Major bubble interaction mechanisms in bubbly flow conditions. |
In Fig. 1, the major phenomenological mechanisms have been identified and appropriate mechanistic models have been established [4,5]:
- Forming a unit, i.e. coalescence through random collision driven by turbulent eddies; eddies are the swirling of a fluid and the reverse current created when the fluid flows past an obstacle, Coalescence due to the acceleration of the following bubble in the wake of the preceding bubble, and Break-up due to the impact of turbulent eddies.
Assessment of models
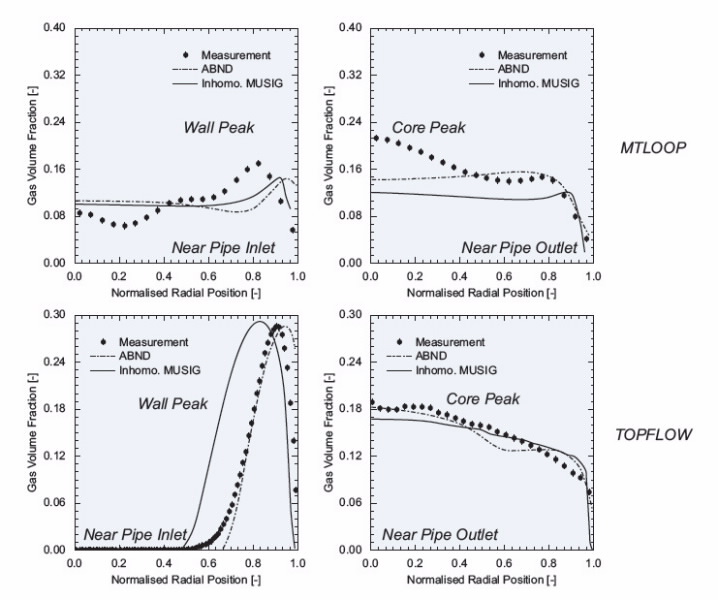 |
| Fig 2. Comparison of the predicted radial gas volume fraction distributions with MTLOOP and TOPFLOW measurements. |
Fig. 2 compares the predicted gas void fraction profiles for a vertical air-water flow against experimental data of MTLOOP [6] and TOPFLOW [7] obtained at Forschungszentrum Rossendorf, Germany.
It can be observed that population-balance models based on ABND and Inhomogeneous MUSIG have been able to capture the transition process from wall peak where the local volume fraction is maximum near the pipe wall to core peak where the local volume fraction is maximum at the pipe centre of the gas-volume fraction distribution.
Tomiyama et al. [8] and Krepper et al. [9] have shown that the lift force which acts perpendicular to the vertical fluid flow is positive when the gas bubbles are small.
These bubbles flow preferentially along the pipe wall. However, the lift force becomes negative when the bubble size is greater than 5.5 – 6.0 mm.
Because of the high bubble coalescence rate that can be experienced near the pipe outlet, the negative lift force pushes the large gas bubbles towards the pipe centre, resulting in the core peak distribution.
Modelling beyond bubbly flow regime
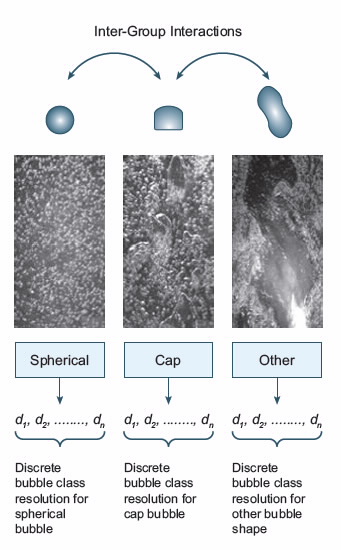
This modelling framework considers additional transport equations to characterise different groups of gas bubbles. For bubbly flow, the bubbles are normally categorised as spherical bubbles.
For flows beyond the bubbly flow regime, the bubbles could be in the form of cap or slug or churn-turbulent. By solving each transport equation to characterise the particular group of bubbles such as described in Fig. 3, such a framework presents great potential of accounting the wide spectrum of bubble sizes that may exist in different flow regimes.
Further work is required to formulate more comprehensive bubble coalescence and break-up models to handle gas-liquid flows beyond the bubbly flow regime.
|
| Fig 3. An illustration of the multi-group multi-bubble-class model. |
Authors
Guan Heng Yeoh1, Sherman Chi Pok Cheung2, Jiyuan Tu2
1ANSTO, 2School of Aerospace, RMIT University
References
- S. C. P. Cheung, G. H. Yeoh and J. Y. Tu (2007). On the modelling of population balance in isothermal vertical bubbly flows - Average bubble number density approach, Chem. Eng. Process., 46, 742-756.
- S. M. Lo (1996). Application of Population Balance to CFD Modelling of Bubbly Flow via the MUSIG model, AEA Technology, AEAT-1096.
- D. L. Marchisio and R. O. Fox (2005). Solution of population balance equations using the direct quadrature method of moments, J. Aerosol Sci., 36, 43-73.
- M. J. Prince and H. W. Blanch, H. W. (1990). Bubble Coalescence and Break-up in Air-Sparged Bubble-Columns,AIChE J., 36, 1485-1499.
- H. Luo and H. Svendsen, H. (1996). Theoretical model for drop and bubble breakup in turbulent dispersions, AIChE J., 42, 1225-1233.
- D. Lucas, E. Krepper and H.-M. Prasser, H.M. (2005). Development of co-current air-water flow in a vertical pipe, Int. J. Multiphase Flow, 31, 1304-1328.
- H.-M. Prasser, M. Beyer, M., H. Carl, S. Gregor, D. Lucas, H. Pietruske, P. Schutz, F. P.Weiss (2007). Evolution of the structure of a gas-liquid two-phase flow in a large vertical pipe, Nuc. Eng. Des., 237,1848-1861.
- A. Tomiyama, Struggle with computational bubble dynamics, Proc. 3rd Int. Conf. Multiphase Flow, Lyon, France (1998).
- E. Krepper, D. Lucas, T. Frank , H.-M. Prasser and P. J. Zwart, P.J. (2008). The inhomogeneous MUSIG model for the simulation of polydispersed flows, Nuc. Eng. Des. 238, 1690-1702.
Published: 15/11/2011