 |
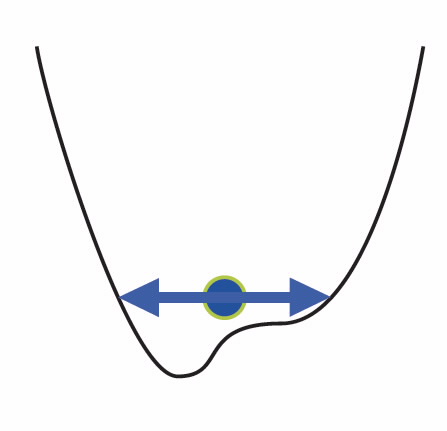
| Fig 1. A cartoon of an atom in an energy well, unable to reach the minimum due to thermal motion. |
Strontium titanate offered few surprises to scientists, until a recent discovery unearthed a world of possibilities for the computer industry and information storage.
Introduction
Strontium titanate (SrTiO3) had been analysed so thoroughly that it appeared it could hold no further secrets. But in 1999, a surprising discovery showed that electric properties of the crystal could be changed simply by increasing the mass of oxygen atoms.
As is usually the case with unexpected phenomena, the explanation lies outside of classical physics and has to be found in the domain of elusive quantum-mechanical effects.
The phenomenon is as puzzling as it is useful: changing the mass of oxygen atoms in the system gives strontium titanate an electronic polarisation and therefore the ability to ‘remember’ its electrical state, yet all we have changed is the nucleus - nothing to do with the electrons.
Understanding the origins of the process could let us modify compounds used in computing and create new options for information storage.
Experiments immediately followed the discovery of electrically polarised strontium titanate and its properties were determined, but produced ambiguous answers to the question of the system’s structure.
It appeared that the static structure of the lattice resulted from the dynamic behaviour of the atoms, and more precisely from the quantum motion that is required by the uncertainty principle. Inelastic neutron scattering is the best tool for studying the dynamic
behaviour of atoms in a crystal, but only by applying computational techniques together with experimental methods can the crucial link between the static and dynamic properties of the crystalline lattice be unravelled.
By using a heavy isotope of oxygen, the crystal can be tricked into the structure that is quantum-forbidden for the 16O crystal. We elucidate [1] the arrangement of atoms in the quantum-forbidden structure and show that its properties are the same as those observed experimentally in the isotopically tricked crystal.
The root of the problem
The way in which atoms arrange themselves in a crystal depends on the amount of thermal energy.
At high temperature the atoms overcome the forces and interactions that distort the internal structure of the crystal at low temperature. At very low temperatures it is the weakest interaction that finally pulls the atoms into their lowest-energy arrangement.
The structural changes that occur as atoms occupy lower energy positions with decreasing temperature are known as phase transitions.
Quantum theory tells us that we cannot know both the energy and the position of particles with perfect accuracy; so what happens if there is a lower-energy arrangement of the atoms that cannot be reached due to this enforced uncertainty?
Fig. 1 [Refer to the image library below]is a schematic illustration of this situation where the uncertainty of position (effectively a quantum motion) keeps the atom at an average position that is different from the lowest-energy position.
Careful analysis of the low-temperature properties of strontium titanate, SrTiO3 (STO), implies that this crystal is indeed such a case. This can be visualised as the atoms vibrating with an uncertainty-amplitude that is too big to fit into the energy minimum (similar to the ball in Fig. 1). Some years ago an interesting experimental trick was found [2] to force STO into this lowest-energy structure.
A regular oxygen nucleus contains 16 nucleons (8 protons and 8 neutrons), but isotopes containing 1 or 2 additional neutrons are also stable and exist in nature, although in much lower concentrations. 17O is well known for its magnetic properties that make it useful in magnetic resonance imaging, and 18O is virtually identical to the regular 16O apart from being heavier by the mass of two neutrons.
By substituting this heavier isotope to get SrTi18O3 (labelled STO18), the quantum uncertainty in atomic position diminishes slightly and a new low-symmetry phase appears below 23 K. The clearest signature of this new phase is the electric field in the crystal even when there is no external electric field applied to it, this being known as a ferroelectric.
The change in symmetry causes the electrons to interact differently with atomic motion which causes new spectra to be seen that also characterise the phase change. Not surprisingly, the change in positions of the atoms at the phase transition is very slight, and so far it has not been possible to determine these new positions experimentally.
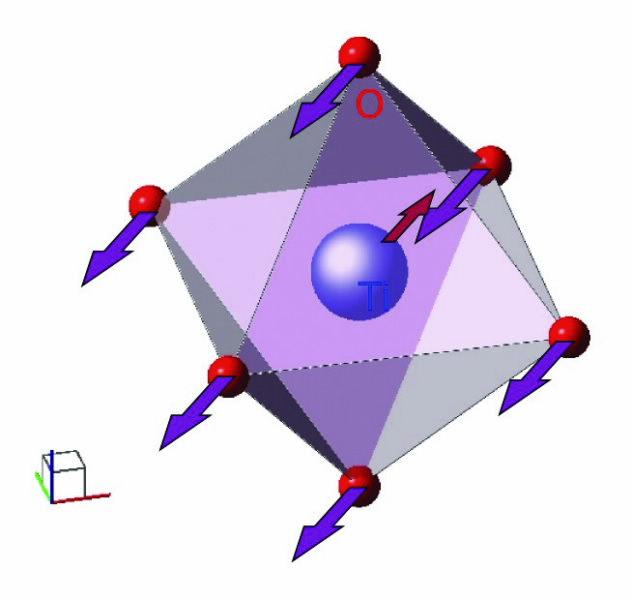 |
| Fig 2. The direction of distortion that makes the ferroelectric structure. |
The route to a solution
This is where computers can really help because they can simulate crystals that reach totally artificial situations - such as the absence of quantum uncertainty.
For this we need to know how the energy of the crystal changes when we move the atoms around inside it.
We used density functional theory (DFT) calculations implemented by Vienna Ab-initio Software Package (VASP [3]).
DFT simulates the state of electrons at absolute zero temperature and can determine ion charges, forces acting on atoms and the total energy of the system.
It can also displace atoms into more favourable positions within a small area around the starting point.
Our calculations started from a tetragonal structure of STO observed in a STO16 sample at 1.5 K temperature, later referred to as Structure 1.
Perhaps surprisingly, when we took all of the thermal energy out of the crystal the atoms did not move to new positions, that is, there was no phase transition.
However by calculating the dynamical properties of the atoms within the lattice (PHONON [4] ) using force constants (like the ones that describe springs) calculated by DFT we found collective motions of the atoms that led to an even lower-energy arrangement of the atoms, that is a phase transition. The atomic motions we found are illustrated schematically in Fig. 2.
The route to comprehension
We have to analyse the result of the calculations in the context of experimental data. These are only available for the 18O substituted crystal and are limited due to the high cost of this substitution, the low temperatures required and the subtlety of the changes.
However, having obtained a computer-generated crystal structure we can easily computer-generate its properties and compare them with those measured experimentally. If they are the same then it is safe to assume that we have found the quantum-forbidden structure of the isotopically normal STO which can be used to make other predictions about the properties of the new phase.
Most important: the new structure is orthorhombic and has no centre of symmetry, therefore satisfying the necessary condition for electric polarisation to be present in the system. Calculated lattice vibrations of the new structure show that there is no lower-energy arrangement possible, and the vibrational frequencies of the atoms are in good agreement with the ones observed experimentally for STO18 by other groups [5] via Raman spectroscopy.
Finally, although crystallography could not solve the structure of the new phase, it could propose most likely candidates [6] based on diffraction patterns.
Our calculated structure corresponds to one of the most likely candidates.
We have confirmed that the atom positions we determined are valid, but now it is time to see if we are right about atom motion.
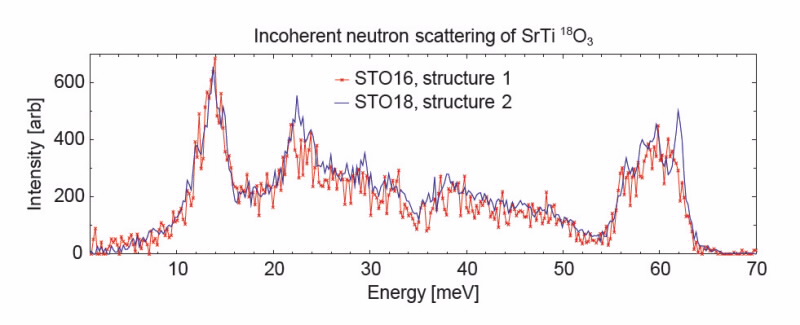
Analysing the lattice vibrations let us predict the result of incoherent neutron-scattering experiments on STO16 and STO18 and we see that the differences in atom vibrations spectra (shown in Fig. 3) of Structures 1 and 2 should be visible in the experiment results.
In future studies we will use Taipan, ANSTO’s triple-axis spectrometer, to measure the incoherent neutron scattering of STO16 and STO18 samples and verify our prediction.
|
| Fig 3. A section of calculated incoherent neutron scattering spectrum of STO16 and STO18 at liquid helium temperature. |
Authors:
M. Bartkowiak1,2, G. J. Kearley1 , M. Yethiraj1 , and A. M. Mulders2
1ANSTO, 2School of Physical, Environmental and Mathematical Sciences, UNSW@ADFA
References:
- Bartkowiak, M., Kearley, G. J., Yethiraj, M., & Mulders, A. M. (2011). Symmetry of ferroelectric phase of SrTi18O3 determined by ab initio calculations. Physical Review B, 83(6), 064102.
- Itoh, M., Wang, R., Inaguma, Y., Yamaguchi, T., Shan, Y. –J., & Nakamura, T. (1999). Ferroelectricity induced by oxygen isotope exchange in strontium titanate perovskite. Physical Review Letters, 82(17), 3540–3543.
- Kresse, G., & Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16), 11169–11186.
- Parlinkski, K. (2003). PHONON software. Retrieved 4 April 2011, from www.computingformaterials.com/index.html
- Shigenari, T., Abe, K., Takemoto, T., Sanaka, O., Akaike, T., Sakai, Y., et al. (2006). Raman spectra of the ferroelectric phase of SrTi18O3: Symmetry and domains below Tc and the origin of the phase transition. Physical Review B, 74(17), 174121.
- Noda, Y., Mochizuki, Y., Kimura, H., Itoh, M., Kyomen, T., & Wang, R. (2005). Possibility of slater-mode condensation in ferroelectric SrTi18O3. Journal of the Korean Physical Society, 46(1), 69-72.
Published: 26/07/2011